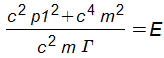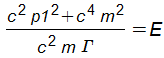425(3): Rigorous Self Consistency of m Theory
Many thanks again for these comments, with which I agree. There is an exact self consistency between Eqs. (26) to (28), giving Eq. (47) twice over. Eq. (47) has already been checked by computer so that is one theme of UFT425. Currently I am reading around the basics of hamiltonain dynamics to make sure that there are no errors of concept. This is the first time that hamiltonian dynamics have been used in the UFT series, apart from the derivation of the quantum Hamilton equation in UFT175 and UFT176. In general, the question being asked is what new information is given by the use of hamiltonian dynamics? One example is Eq. (47). As shown in examples worked out by Marion and Thornton, lagrangian and hamiltonian dynamics are used together, so in the next note I will write out these examples to show what I mean, and apply them to orbital theory.
425(3): Rigorous Self Consistency of m Theory
To: Myron Evans <myronevans123>
Thanks, I can follow now the derivation of (36). Concerning eqs. (53-56) for the rest particle, a particle in a Coulomb-like potential cannot be at rest, only for the two return points of the orbit. Are these points meant here? Or a particle fixed by a constraint?
Eqs.(64/65) seem to contain typos. Eq. (57) for the inertial system is
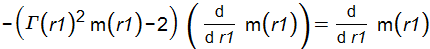
This has two solutions:
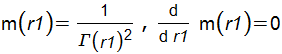
I do not find the solutio (67). The Hamiltonian (68) seems simply to be the non-relativistic version of m theory in space (r1, phi).
Eq. (100) leads to
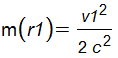 ,
,
a factor of 1/2 seems to be missing. It is to be considered that this m function may be far away from unity for the inertial system, perhaps not very realistic.
Finally I would like to comment that in case of the approximation gamma=const eq. (57) may be solved, giving a transcendent solution. In the case of the inertial system the integration constant can be determined from the condition
m(r1_0) = m_0
Horst
Am 21.12.2018 um 06:20 schrieb Myron Evans:
425(3): Rigorous Self Consistency of m Theory
OK thanks, Eq. (36) was first derived as Eq. (19) of UFT424 and looks OK. Rearrange Eq. (33) as:
gamma squared m(r1) m squared c fourth = p1 squared c squared+ m squared c fourth
and use
E squared = m(r1) squared m squared c fourth gamma squared
to get Eq. (36). To triple check this can be run through the computer.
425(3): Rigorous Self Consistency of m Theory
To: Myron Evans <myronevans123>
I do not understand how (36) is derived from (35) and (33). When rewriting (33) in such a way that the term (35) for E can be inserted, I obtain the result
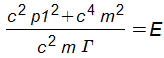
which depends on gamma. How can I get rid of gamma? Inserting the definition gives an unwanted dependence of v1.
Horst
Am 20.12.2018 um 12:31 schrieb Myron Evans:
425(3): Rigorous Self Consistency of m Theory
This note is a detailed demonstration of the rigorous self consistency of m theory in the elegant Euler Lagrange Hamilton dynamics. This is the first time that detailed consideration has been made of Hamilton’s equations in the UFT series. The self consistent choice of the Hamilton canonical variables is given in Eqs. (27) and (28). This gives the Einstein energy equation (36) in m space, first derived in UFT424. Eq. (47) is obtained in a rigorously self consistent manner from both Eqs. (42) and (43). This checks the starting equation of Note 425(2). The static solution is rigorously equivalent to the rest energy (56) of m theory. The static solution is for a particle m at rest attracted gravitationally by a particle M at rest in m space. The general solution is Eq. (57) and in the inertial frame gives the remarkable result (68) for the hamiltonian, reducing it to classical format in m space. The first Evans Eckart equation reduces this to the force equation in m space in an inertial frame, Eq. (76), giving a new definition of vacuum force, Eq. (80). The hamiltonian can be transformed to plane polar coordinates (r1, phi) giving Eq. (88). Finally the solution obtained in Note 425(2), and checked by computer algebra, is given in Eq. (93) in plane polar coordinates (r1, phi). This related dm(r1) / dr1 to M(r1). This is very complicated equation but can be solved as discussed by Horst this morning. The final note for UFT425 will be considered in the next and final note, using the second Hamilton equation. This is an entirely new classical dynamics valid for any m space.
425(3a).pdf
425(3)-gamma=const.pdf
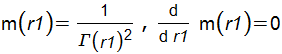
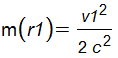 ,
,