Alpha Institute for Advanced Studies

The fundamental problem of Einstein’s field equation is as follows. At the left, you have the Einstein tensor which is pure geometry. At the right, you have the energy-momentum or – better – stress-energy or energy-density tensor, which is independent of the curvature field. Therefore, the latter tensor does not contain the field energy.
(see https://math.ucr.edu/home/baez/physics/Relativity/GR/energy_gr.html)
Therefore, Einstein’s theory had some success for explaining small deviations from special relativity in the solar system, but fails, for example, in explaining the velocity curves of galaxies.

Besides this, the approach (“ansatz”) of Einstein’s equation has consequences for the mathematics. The geometric quantities of the left hand side are equated to a physical definition on the right hand side which does not come from geometry so that the region of Riemann geometry is left. In doing so, one has to guarantee that no contradictions appear. However, when Riemann geometry is embedded into a “more complete” geometry, namely Cartan geometry, it comes out that Einstein’s approach leads to contradictions. His approach is only valid as a rough approximation to the higher-level geometry, where torsion is considered to be a minor disturbation.
Heim recognized this problem of Einstein’s equation without using formal arguments like Cartan geometry.

Heim published only few papers and most of his heritage is written on notice sheets. His computation of masses of elementary particles is not well documented, I never tried to understand this, although the results are convincing.

Gauge theory is not compatible with Cartan geometry. Gauge theory leans on a zero photon mass, which leads to a truncated form of electromagnetic waves (no longitudinal waves). However, longitudinal wave solutions are compatible with Maxwell’s equations. This is an argument that photn mass exists, and this falsifies gauge theories. Cartan theory delivers the Proca equation, which is the mathematical formulation that gauge invariance does not exist, and of course longitudinal waves are solutions of Cartan geometry. This is an argument for me that the extension of Riemann geometry by Cartan geometry is a good choice.

Thanks, Kerry, for these clarifications.
ECE2 theory offers indeed a connection to Einstein’s general relativity, so “Trojan horse” is justified. In this context, UFT paper 445 should be mentioned. Doug and I have shown that Einstein’s field equation, although strictly mathematically wrong, can be considered as an approximation to Cartan geometry, when torsion is considered as a higher-order perturbation. This is another “Trojan horse”. We only need some Greeks who bring in the horse to Troja (i.e., the world of standard physics :-).

Horst

—————————

Chapter 6 of your book introduces us to ECE2 theory.

It allows for simplification by reducing the need to refer to tangent space, when dealing with curvature. However, torsion is still incorporated in the background.

I like page 118, where the pure curvature equations of ECE2 take the guise of Einstein’s general telativity, while the geometric current definitions contain a torsion term allowing for Cartan geometry to enter from stage left.

So ECE2 theory carries the Trojan horse to open up general relativity to a new millenium treatment, which allows for calculations of fields to be better defined.

Best wishes

Kerry Pendergast

I was asked how charge and mass of matter is handled in Heim’s generalized field theory.

Heim uses Einstein’s field equation and defines a (generalized) energy-momentum tensor for this purpose, which contains electromagnetic and gravitational components. The gravitational components are defined in analogy to the electromagnetic components and contain the gravito-magnetid field, for example. The problem, however, is that the energy-momentum tensor contains charge and mass density terms. In this way, Einstein’s field equations become dependent on explicit sources. This leads to problems of several kinds, in particlular a physical interpretation problem of sources in general relativity, and, as far as I know, abolition of energy conservation.

Heim tries to avoid these problems by assuming that sources are nothing else than “compacted” fields. I cannot say how he treats this formally. Evans avoids this problem in his ECE theory in the same way, but Evans does not use Einstein’s field equations, he uses the geometry equations of Cartan instead. This approach avoids all the problems that Einstein had. There are no sources a priori but only fields, as Heim assumed. In ECE theory, the equations of Cartan geometry can be written in a form equivalent to Maxwell’s equations, for electrodynamics as well as for gravitation. By comparing with Maxwell’s original equations with chages and currents, one can define charge and current terms, which consist of field terms mixed with curvature and torsion terms. The same can be done for gravitation. Unification happens via geometry. If a charge is there, we have electromagnetism, if not, we have gravitation only.

Heim and Evans agree in the point that they do not need sources in their theories. Matter is a “condensed field” of general relativity and spacetime itself may be interpreted as a vacuum or aether field being everywhere. To my understanding, Heim’s theory could be put on a much clearer ground if it would be based on Cartan geometry rather then Einstein’s field equations.
Considering matter as condensed fields leads to quantum mechanics in a straight line, avoiding extra concepts like quantum electrodynamics and similar. According to Evans, all physics is geometry.

Dear Kerry,

the gravitational constant has to do with the aether density, because the latter is connected with gravitation. According to the paper under development, it is a special counter-effect to electromagnetism.
The relativists have shown that Einstein’s cosmological constant obeys the relation
Λ = 8 π ρ_vac G / c⁴ = κ ρ_{vac .}
kappa is related to the gravitational constant G, and rho_vac is the energy density of the vacuum. However, this is very, very low compared to an aether density. This is similar to the ECE equation



where G connects the matter density with its field. Accordign to Eq. (8.285) of the text book,

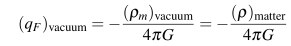
G is the factor between vacuum density and mechanical “vacuum charge” q_F. The primordial voltage connects geometry and electromagnetism directly. I would rather compare G with the electromagnetic constants epsilon_0, mu_0. There is also a primordial gravitational constant Q(0), see Eq. (7.21) of the text book.

Horst


Am 13.12.2021 um 16:29 schrieb kerry pendergast:

Dear Horst,

Would you agree that the gravitational constant is arbitrary and determined by the mean density of matter in the universe.

Then the primordial voltage defined by torsion in ECE theory, comes from the mean density of matter in the universe.

Kerry



On Monday, 13 December 2021, kerry pendergast <pendergastkerry@gmail.com> wrote:
> Fred Hoyle is famous as a proponent of the steih ady state theory.
>
> In a radio broadcast in March 1949, Hoyle coined the term Big Bang theory, which caught on around the world in the 70s.
>
> In 1979, I got as far as an interview to join his team in Cardiff University.
>
> However, by then their interest was not on the big bang, but on detecting and identifying interstellar molecules in cosmic dust in space. This is why they needed a chemist.
>
> Kerry

In Paper 446 on the AIAS web site, theoretical considerations have been made to realize counter gravitation and harvest energy from spacetime itself. The momentum of the electromagnetic field is used to counteract gravitation. The result is similar to the force an electron experiences in a capacitor volume which is the basis for the well known Millikan experiment.

Secondly, a resonance mechanism of the harmonic oscillator is described, where the electromagnetic vector potential is used to create mechanical resonance so that energy from the vacuum or spacetime can be transferred. For a net win of energy, it must be ensured that there is no backward dependency from the oscillator, while the vector potential is utilized or created. One possibility is to use the vector potential of permanent magnets, which is “refilled” automatically by quantum processes, if this field is doing external work.