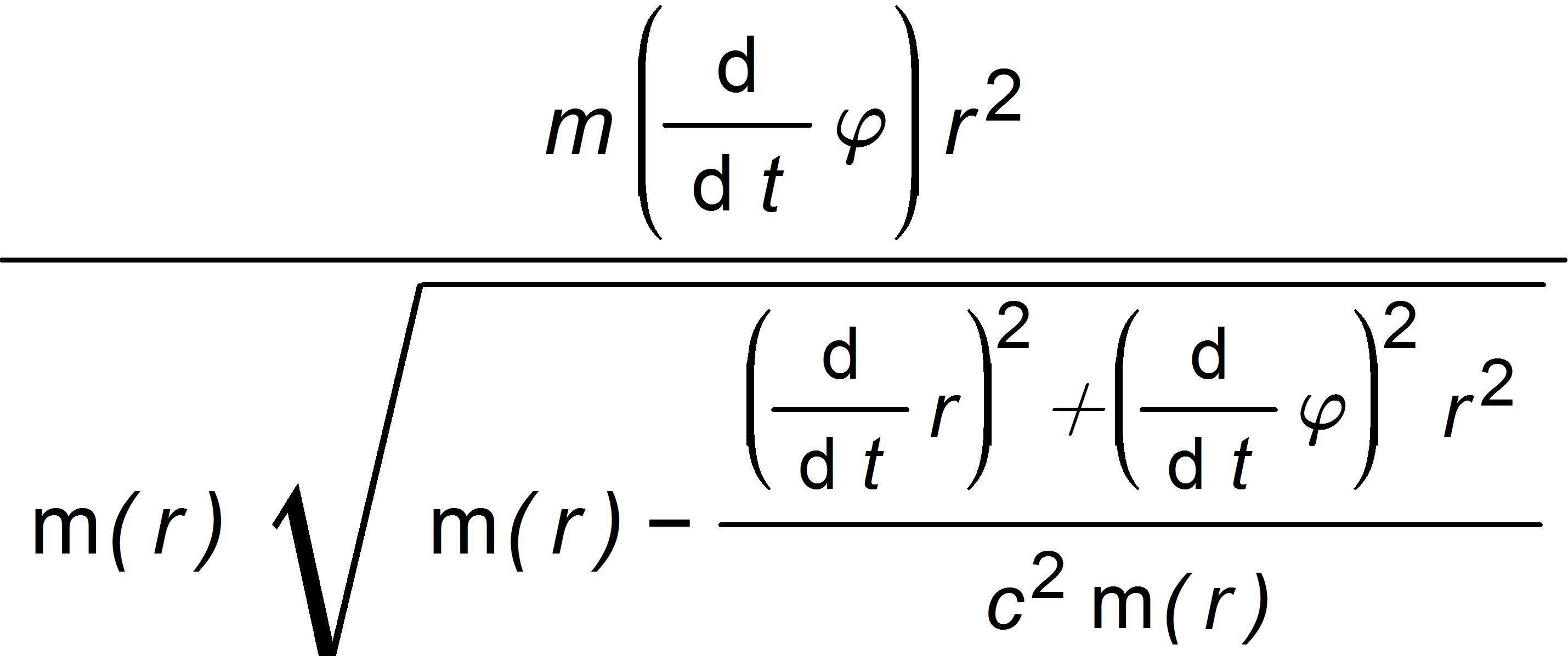Note 424(1): Derivation of the Lagrangian of m Theory from the Hamiltonian
Thanks for going through this, the right method emerged in the latter part of Note 424(3), using the frame (r1, phi). This was used in the final Sections 1 and 2 of UFT424 posted on www.aias.us. The geodesic method of Note 424(2) was used to check the hamiltonian. Then in Note 425(1) a self consistent methodology was found, and now I am working on the Hamilton canonical equations for m theory. So it is now known that the lagrangian and hamiltonian of m theory are rigorously self consistent in frame (r1, phi), the frame of m space using the fundamental concepts of Euler Lagrange Hamilton dynamics. This is not true in the frame of flat space (r, phi).
Note 424(1): Derivation of the Lagrangian of m Theory from the Hamiltonian
To: Myron Evans <myronevans123>
The calculations are o.k. If see it right, the Lagrangian (19) should give the same equations as obtained from
dH/dt = 0,
dL/dt = 0.
Will check this. As I see this, the Hamiltonian is eq.(11) and the potential energy should contain the m(r) factor:
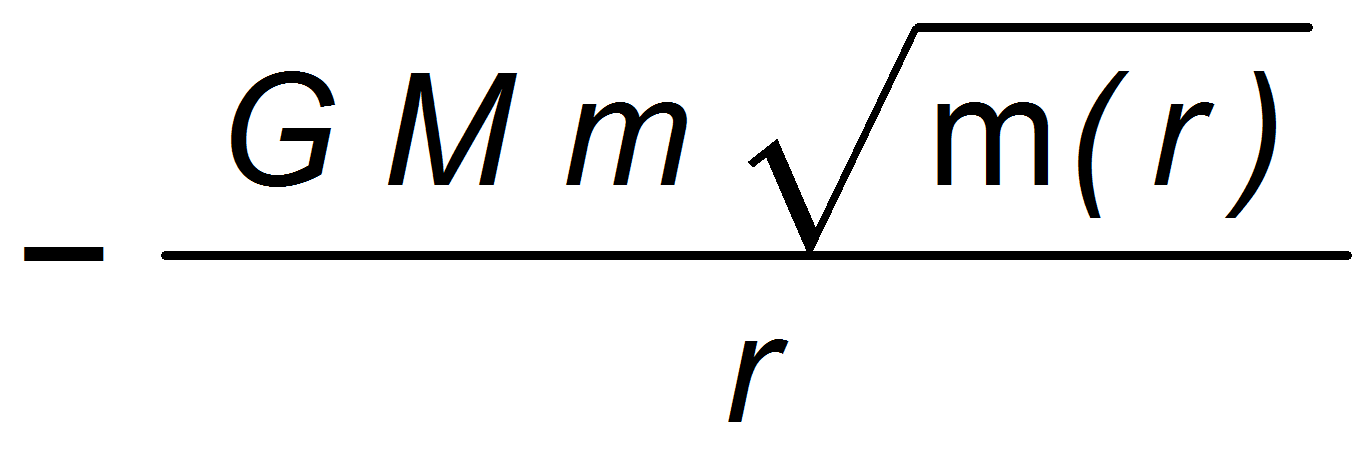
.
Horst
Am 08.12.2018 um 14:39 schrieb Myron Evans:
Note 424(1): Derivation of the Lagrangian of m Theory from the Hamiltonian
The lagrangian is Eq. (19), and is derived from the hamiltonian using the fundamental equation (1) of Lagrangian dynamics. The lagrangian is therefore rigorously equivalent to the hamiltonian and to the Evans Eckardt equations. This is an entirely new physics so a vast amount of new information is given by it. From now on I suggest using both hamiltonian and lagrangian methods. The first thing to do is to derive orbits, superluminal motion, energy from m space, and all previous results of UFT415 ff from the Evans Eckardt equations by solving dH / dt = 0 and dL / dt = directly without using the lagrangian. The rigorously correct lagrangian is now known and the Euler Lagrange equations (22) and (23) will give additional equations which must be equivalent to the Evans Eckart equations. This will lead to several new constraint equations such as (34). The rigorously correct lagrangian (19) reduces to the lagrangian used initially by inspection in the limit m ( r ) goes to one, but not identically equal to one. The Hamilton canonical equations can also be used at a later stage and quantization can be initiated. With the computer, any amount of complexity is no problem.