Alpha Institute for Advanced Studies

Computation of the Valence Charge Density of the Nickel Atom

This is an exceedingly interesting development, this program applies computational quantum chemistry to the m theory and finds an effect on the valence structure of the nickel atom. It is a small effect as expected, but nevertheless it is a real effect, similar to the Lamb shift, also a small effect. So the generally relativistic quantum mechanics can be coded up in computational quantum chemistry, and applied to a vast number of problems. This program can be used to develop the m theory far in advance of analytical solutions of the Schroedinger equation. The latter is analytical only for the H atom, as is well known. For the helium atom onwards, computational methods have to be used. It would be interesting to apply this program to a proton interacting with the nickel atom, using m theory. That might lead to low energy nuclear reaction. I think that thi sis a big step forward and this program can be used in many ways.

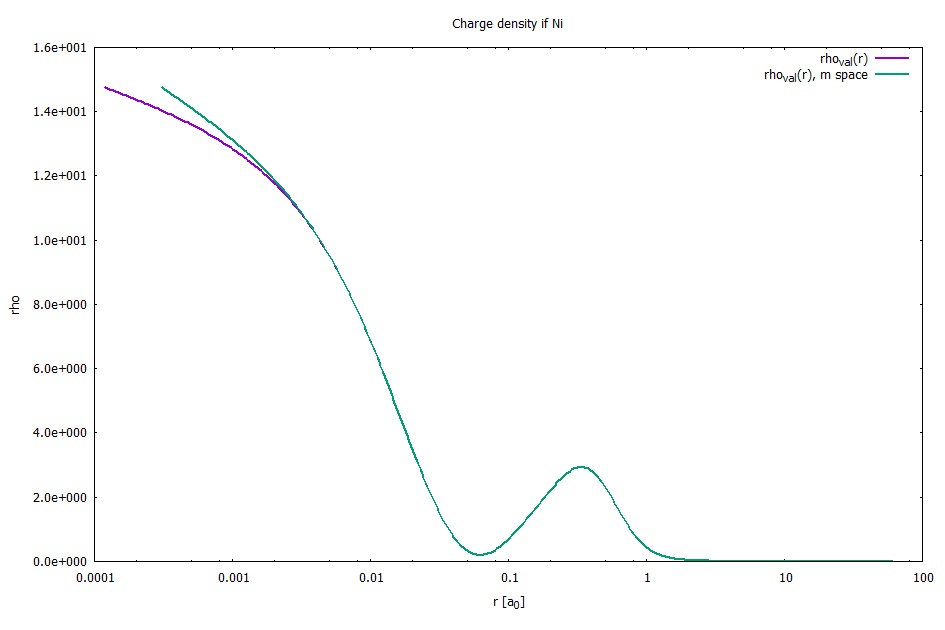
The effect of m space is that the wave functions psi(r) are shifted to the outer region by

psi(r) –> psi( r/sqrt(m(r)) )

because

r/sqrt(m(r)) >= r.

I succeeded in reactivating an old electronic structure program for atoms which a colleague at the TU Clausthal sent me years ago. I calculated the charge density of a Ni atom. The valence charge density (10 electrons) is graphed in the file, in original form and with shifted radius coordinate as above. One has to make the parameter R of the m function quite large to find a visible effect.
I hope that jpg files go through the wordpress upload better than png files.

Horst

Am 07.04.2019 um 09:31 schrieb Myron Evans:

436(4) : General Solution of the Schroedinger Equation

This is given by Eq. (8) and several examples given. In the usual vacuum free quantum mechanics the expectation value of energy from Eq. (8) is given by <E> = E, but in quantum mechanics in m space (or the vacuum), i.e. generally covariant quantum mechanics, the energy levels are shifted according to Eq. (31). This is a general law of quantum mechanics, true for any spectral line.

436(4) : General Solution of the Schroedinger Equation

This is given by Eq. (8) and several examples given. In the usual vacuum free quantum mechanics the expectation value of energy from Eq. (8) is given by <E> = E, but in quantum mechanics in m space (or the vacuum), i.e. generally covariant quantum mechanics, the energy levels are shifted according to Eq. (31). This is a general law of quantum mechanics, true for any spectral line.

a436thpapernotes4.pdf

436(3): General Law for the Spectral Effect of the Vacuum

The Planck law is changed to Eq. (11) for any spectral line. The extent of the change is controlled by an integral over an m(r) power half function. In the presence of the vacuum the relation between energy and frequency, E = h bar omega,is changed fundamentally, because the geometry is fundamentally different.

a436thpapernotes3.pdf

To Prof. Steve Bannister, University of Utah,

The Effect of the Vacuum on Physics

This is indeed the case. The vacuum is ever present and manifests itself in many different ways. The m theory is general relativity merged with quantum mechanics in a straightforward way. The best known effect of the vacuum in quantum mechanics is the Lamb shift, this has been explained using m theory by Horst Eckardt and myself without using quantum electrodynamics, and without using the Heisenberg uncertainty principle to create virtual particles. The m theory must always be tested against experimental data of course, it is not just pure mathematics. The m(r) function develops the infinitesimal line element and the metric in a well defined way. This is exactly the method used by Einstein to develop the original but torsionless, general relativity. He used the function m(r) = 1 – r0 / r. So general relativity can be viewed as a a vacuum effect, the vacuum being understood in terms of the departure of the metric from the Minkowski metric. The standard treatment of the Lamb shift relies on things that cannot be tested experimentally, for example virtual particles which can never be observed, and are created in an unknowable way. QED also removes infinities by renormalization, and uses dimensional regularization. These are non Baconian procedures, which involve adjustables. The standard people claim that QED is a precise theory, but clearly it cannot be a Baconian theory at all. The latest m theory is very simple, it starts with the most fundamental entity in quantum mechanics, the wave function.

Myron,

Is it correct then, given m theory, that it is never right to ignore vacuum effects in any quantum calculation?

Thanks,

Steve

Stephen C. Bannister, Ph.D. Director, MIAGE Associate Director, Economic Evaluation Unit, Macroeconomics Assistant Professor, Economics University of Utah Fellow, AIAS. "Ubi materia ibi geometria"

On 4/5/2019 3:07 AM, Myron Evans wrote:

The m Theory of the Anharmonic Oscillator

The anharmonic oscillator has energy levels (1) in the usual quantum mechanics. These are modified to Eq. (6) in m theory, giving the effect of the vacuum.The Morse potential is used for the anharmonic oscillator because when used in the Schroedinger equation gives exact solutions. The usual solution for energy is Eq. (5) in the vacuum free quantum mechanics, and is modified to Eq. (6) by the vacuum. "The vacuum" is defined by the m(r) function, i.e. by a change of geometry. The vacuum free wave functions of the anharmonic oscillator are given by Eq. (13), and are modified by the vacuum using the usual rule (15). The wave functions look very complicated but can be evaluated with computer packages. They are defined by the generalized Laguerre polynomials and the Kummer confluent hypergeometric function (14) for each vibrational quantum number n. The radial part of the wave functions of the H atom are also defined in terms of Laguerre polynomials, and are modified by the vacuum through the same rule (15). It would be interesting to graph the effect of the vacuum on the wavefunctions of these well known problems, and indeed any problem of quantum mechanics, using if necessary packages of computational quantum mechanics, of which there are many available in code libraries.

To Prof. Steve Bannister, University of Utah,

The Effect of the Vacuum on Physics

This is indeed the case. The vacuum is ever present and manifests itself in many different ways. The m theory is general relativity merged with quantum mechanics in a straightforward way. The best known effect of the vacuum in quantum mechanics is the Lamb shift, this has been explained using m theory by Horst Eckardt and myself without using quantum electrodynamics, and without using the Heisenberg uncertainty principle to create virtual particles. The m theory must always be tested against experimental data of course, it is not just pure mathematics. The m(r) function develops the infinitesimal line element and the metric in a well defined way. This is exactly the method used by Einstein to develop the original but torsionless, general relativity. He used the function m(r) = 1 – r0 / r. So general relativity can be viewed as a a vacuum effect, the vacuum being understood in terms of the departure of the metric from the Minkowski metric. The standard treatment of the Lamb shift relies on things that cannot be tested experimentally, for example virtual particles which can never be observed, and are created in an unknowable way. QED also removes infinities by renormalization, and uses dimensional regularization. These are non Baconian procedures, which involve adjustables. The standard people claim that QED is a precise theory, but clearly it cannot be a Baconian theory at all. The latest m theory is very simple, it starts with the most fundamental entity in quantum mechanics, the wave function.

Myron,

Is it correct then, given m theory, that it is never right to ignore vacuum effects in any quantum calculation?

Thanks,

Steve

Stephen C. Bannister, Ph.D. Director, MIAGE Associate Director, Economic Evaluation Unit, Macroeconomics Assistant Professor, Economics University of Utah Fellow, AIAS. "Ubi materia ibi geometria"

On 4/5/2019 3:07 AM, Myron Evans wrote:

The m Theory of the Anharmonic Oscillator

The anharmonic oscillator has energy levels (1) in the usual quantum mechanics. These are modified to Eq. (6) in m theory, giving the effect of the vacuum.The Morse potential is used for the anharmonic oscillator because when used in the Schroedinger equation gives exact solutions. The usual solution for energy is Eq. (5) in the vacuum free quantum mechanics, and is modified to Eq. (6) by the vacuum. "The vacuum" is defined by the m(r) function, i.e. by a change of geometry. The vacuum free wave functions of the anharmonic oscillator are given by Eq. (13), and are modified by the vacuum using the usual rule (15). The wave functions look very complicated but can be evaluated with computer packages. They are defined by the generalized Laguerre polynomials and the Kummer confluent hypergeometric function (14) for each vibrational quantum number n. The radial part of the wave functions of the H atom are also defined in terms of Laguerre polynomials, and are modified by the vacuum through the same rule (15). It would be interesting to graph the effect of the vacuum on the wavefunctions of these well known problems, and indeed any problem of quantum mechanics, using if necessary packages of computational quantum mechanics, of which there are many available in code libraries.

The m Theory of the Anharmonic Oscillator

The anharmonic oscillator has energy levels (1) in the usual quantum mechanics. These are modified to Eq. (6) in m theory, giving the effect of the vacuum.The Morse potential is used for the anharmonic oscillator because when used in the Schroedinger equation gives exact solutions. The usual solution for energy is Eq. (5) in the vacuum free quantum mechanics, and is modified to Eq. (6) by the vacuum. "The vacuum" is defined by the m(r) function, i.e. by a change of geometry. The vacuum free wave functions of the anharmonic oscillator are given by Eq. (13), and are modified by the vacuum using the usual rule (15). The wave functions look very complicated but can be evaluated with computer packages. They are defined by the generalized Laguerre polynomials and the Kummer confluent hypergeometric function (14) for each vibrational quantum number n. The radial part of the wave functions of the H atom are also defined in terms of Laguerre polynomials, and are modified by the vacuum through the same rule (15). It would be interesting to graph the effect of the vacuum on the wavefunctions of these well known problems, and indeed any problem of quantum mechanics, using if necessary packages of computational quantum mechanics, of which there are many available in code libraries.

a436thpapernotes2.pdf

436(1): The Harmonic Oscillator in m Theory (i.e. General Relativity)

436(1): The Harmonic Oscillator in m Theory (i.e. General Relativity)

These numerical results are full of interest as usual, I agree that the one dimensional del squared operator is sufficient. The distorted wavefunctions you have graphed imply new energy levels and shifts in energy levels due to m space, i.e. shifts due to "the vacuum" or the nature of space itself. A detailed Google search will probably bring up many items on the Lamb shifts of vibrational type spectra. A more advanced development of the harmonic oscillator brings in the creation and annihilation operators used in photonics (M. W. Evans and S. Kielich (eds.), "Modern Nonlinear Optics" first and second editions, (Wiley Interscience, New York.)

This is an interesting development. I am not sure whether the 3-dimensional harmonic oscillator has to be used in our case where the Laplace operator for r takes a different form than in one dimension, and so will do the solutions.
I have plotted the wave function (26) with the exponential m function we used. Im1.png shows the undistorted eigenstates (with y), Im2.png the distorted eigenstates (with y_1). Obviously the wave function is stretched at r=0 or gets a tip.

Horst

Am 04.04.2019 um 10:02 schrieb Myron Evans:

436(1): The Harmonic Oscillator in m Theory (i.e. General Relativity)

The harmonic oscillator is probably one of the most important features of quantum mechanics and quantum field theory, and this note develops it in m space, or equivalently in general relativity, using the methods of UFT435. It is shown that the energy levels of the harmonic oscillator in m space are given by Eq. (28). Depending on the value of m(r), there are more energy levels than n the usual non relativistic development of the harmonic oscillator. These new energy levels can be thought of as the effect of the vacuum on the harmonic oscillator. For example the effect of the vacuum on vibrational spectra of atoms and molecules. this note shows in yet another way that there is energy in the vacuum (defined as m space).

436(1): The Harmonic Oscillator in m Theory (i.e. General Relativity)

These numerical results are full of interest as usual, I agree that the one dimensional del squared operator is sufficient. The distorted wavefunctions you have graphed imply new energy levels and shifts in energy levels due to m space, i.e. shifts due to "the vacuum" or the nature of space itself. A detailed Google search will probably bring up many items on the Lamb shifts of vibrational type spectra. A more advanced development of the harmonic oscillator brings in the creation and annihilation operators used in photonics (M. W. Evans and S. Kielich (eds.), "Modern Nonlinear Optics" first and second editions, (Wiley Interscience, New York.)

This is an interesting development. I am not sure whether the 3-dimensional harmonic oscillator has to be used in our case where the Laplace operator for r takes a different form than in one dimension, and so will do the solutions.
I have plotted the wave function (26) with the exponential m function we used. Im1.png shows the undistorted eigenstates (with y), Im2.png the distorted eigenstates (with y_1). Obviously the wave function is stretched at r=0 or gets a tip.

Horst

Am 04.04.2019 um 10:02 schrieb Myron Evans:

436(1): The Harmonic Oscillator in m Theory (i.e. General Relativity)

The harmonic oscillator is probably one of the most important features of quantum mechanics and quantum field theory, and this note develops it in m space, or equivalently in general relativity, using the methods of UFT435. It is shown that the energy levels of the harmonic oscillator in m space are given by Eq. (28). Depending on the value of m(r), there are more energy levels than n the usual non relativistic development of the harmonic oscillator. These new energy levels can be thought of as the effect of the vacuum on the harmonic oscillator. For example the effect of the vacuum on vibrational spectra of atoms and molecules. this note shows in yet another way that there is energy in the vacuum (defined as m space).

436(1): The Harmonic Oscillator in m Theory (i.e. General Relativity)

The harmonic oscillator is probably one of the most important features of quantum mechanics and quantum field theory, and this note develops it in m space, or equivalently in general relativity, using the methods of UFT435. It is shown that the energy levels of the harmonic oscillator in m space are given by Eq. (28). Depending on the value of m(r), there are more energy levels than n the usual non relativistic development of the harmonic oscillator. These new energy levels can be thought of as the effect of the vacuum on the harmonic oscillator. For example the effect of the vacuum on vibrational spectra of atoms and molecules. this note shows in yet another way that there is energy in the vacuum (defined as m space).

a436thpapernotes1.pdf

435(6): Rules for Quantization in m Space

This looks very promising and is a sign that the theory is well founded in the fact that the wavefunction is the most fundamental quantity in quantum mechanics. The method can be applied to any wavefunction.

Using eq.(10) with the Hydrogen wave functions, the Lamb shift will come out correctly. According to the term schemes, the Lamb-shifted binding energies are higher on scale than the unshifted energies (i.e. their absolute values slightly decrease). I will produce a diagram tomorrow.

Horst

Am 31.03.2019 um 13:51 schrieb Myron Evans:

435(6): Rules for Quantization in m Space

I arrived at Note 435(6) using the same transformation rules throughout. In all occurrences r is replaced by r / m(r) power half and t is replaced by m(r) power half t. It follows that psi (r, t) of Eq. (4) is replaced by psi(r, t) of Eq. (5). The quantization rules remain the same, because the frame (r, phi) is the same. The state of the particle is completely described by its wavefunction, so I decided to start the analysis with the wavefunction, and to replace r by r / m(r) power half and t by m(r) power half t inside the wavefunction. This gives Eq. (5), in which psi is a function of r and t. So the quantization rules are Eq. (2) and (3) because they are defined in frame (r, t) and psi is defined in terms of r and t. This procedure leads to the modified Planck quantization (10), which uses the expectation value of m power half computed self consistently with the wavefunction (5). This leads self consistently to Eq. (15), which is an equation for the quantized m(r) power half. This philosophy is based on the fundamental role of the wavefunction. The Born normalization remains the same. Since all this is completely new to physics, there is no precedent, so any self consistent procedure can be used. As usual, experiments must decide whether the results are acceptable or not.